How To Find Mrs From Utility Function

Waffles and calzones
- i. Figure out the feasible prepare (or upkeep line) and the marginal rate of transformation (MRT)
- two. Employ calculus and prices to figure out the marginal charge per unit of exchange (MRS)
- three. Ready the upkeep line equal to the price-attuned MRS and employ algebra to solve for $x$ and $y$
- tl;dr Desmos version
Waffles and calzones with different values
- Example 1
- Example 2
- Example 3

The goal of maximizing utility is finding where the ideal meets reality, or where you can be the happiest given your constraints and scarcity. Oftentimes we talk about constraints with budgets, since working with dollars is easier than thinking about factory output or grades, similar you saw in your ESPP reading.

When we talk near "reality" and "ideal" hither, we mean ii dissimilar things:

The feasible set (too known every bit the product possibility frontier or budget line): this represents the bodily tradeoffs between two goods and the constraints on your choices. We've seen this with the aeroplane production functions (where there's a tradeoff betwixt workers and planes) and with Alexei's decision to study (where there'due south a tradeoff between hours of complimentary time and his grade).

The slope of this line is known as the marginal rate of transformation (MRT), or the rate at which you tin can transform workers to planes or written report hours to grades. The slope of this line is also the opportunity cost.
Indifference curves: these correspond the theoretical tradeoff of two goods and your individual preferences. Each curve shows the combination of goods that produce the same level of utility.

The slope of this line is known as the marginal rate of substitution (MRS). It can be written a bunch of other ways:

\[ MRS = \frac{dy}{dx} = \frac{\Delta y}{\Delta x} = \frac{\text{Price}_x}{\text{Price}_y} = \frac{MU_x}{MU_y} = \frac{\fractional u / \partial x}{\partial u / \partial y} \]

We can find the optimum combination of goods (workers and planes, hours and grades, etc.) by combining the feasible set with indifference curves. With some algebra and calculus, nosotros tin notice the combination of goods that maximizes utility, or detect which indifference curve is tangent to the feasible set/upkeep line.

Don't worry if you can't remember calculus! You tin use Wolfram Alpha to observe derivatives automatically, or consult Khan Academy for a review of the power rule and computing partial derivatives.

Here'southward the full general process for maximizing utility:

Effigy out the feasible gear up (or upkeep line) and the marginal rate of transformation (MRT)
Utilize calculus and prices to effigy out the marginal rate of substitution (MRS)
Set the budget line equal to the price-attuned MRS and use algebra to solve for $ten$ and $y$

Waffles and calzones

For this example, let's pretend that you take to decide how many waffles and calzones to eat to brand you the happiest possible. You accept $20 to spend. What do yous do?! Allow's write out the question more formally:

Imagine that waffles (x) cost $ane and calzones (y) cost $2. You have a food upkeep of $xx. Your utility function for waffles and calzones is $u = xy$.

Here'south how to effigy this all out:

1. Figure out the feasible ready (or budget line) and the marginal rate of transformation (MRT)

In this case our viable set is not a production function—we aren't limited past workers or fourth dimension. Instead, nosotros're express past our budget. We tin just spend $twenty. If we spend all our money on calzones, we could buy 10 of them. If nosotros spend all our money on waffles, we can buy xx of them. We can plot all the combinations of waffles and calzones as a upkeep line:

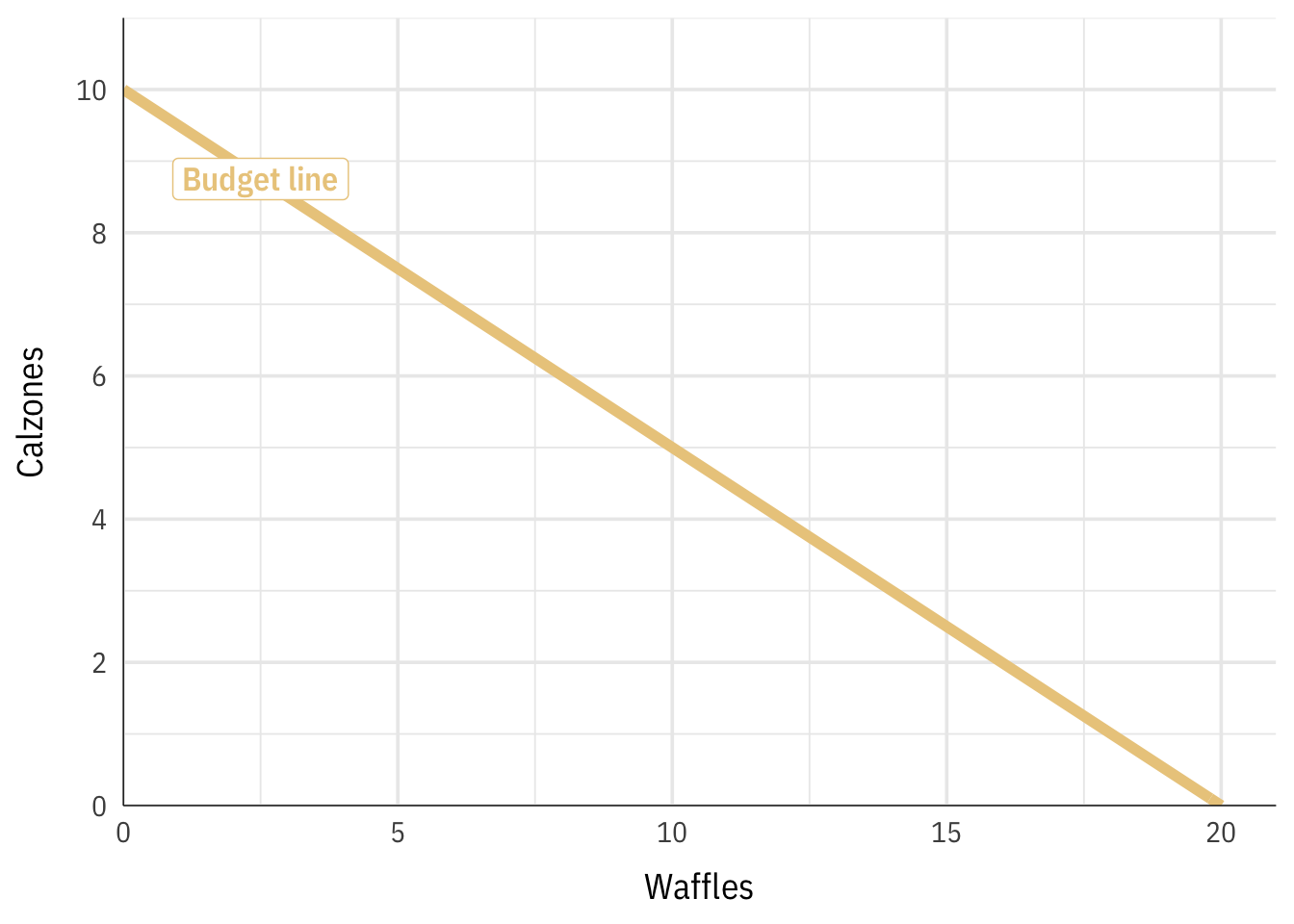
We tin write this budget line as an equation following the $y = mx + b$ format, where $m$ is the slope and $b$ is the y-intercept. The slope here is the marginal rate of transformation (MRT).

\[ y = -\frac{one}{2} x + 10 \]

2. Use calculus and prices to figure out the marginal rate of commutation (MRS)

We can afford every combination of waffles and calzones along the budget line, but we don't know what the optimal mix of waffles and calzones is—that depends on how much nosotros like the two foods, or our preferences.

Our utility function is $u = xy$, which means that we multiply the quantity of waffles and calzones together to get our utility. That is, if we eat 10 waffles and iv calzones, nosotros'll go 40 utils; if we consume v waffles and 14 calzones, we'll get 70 utils; and so on.

Indifference curves show all the combinations of two goods that provide the aforementioned utility. If we want to get 40 utils, we could eat 20 waffles and 2 calzones, 10 waffles and 4 calzones, 5 waffles and 8 calzones, etc. Each of those combinations provides 40 utils of happiness.

We can summate the combinations of waffles and calzones that lead to whatsoever amount of utility. In the chart below, I show three dissimilar indifference curves. Every point along the curve represents the combination of waffles and calzones that would atomic number 82 to x, 20, and 40 utils.

Adjacent, we tin use this utility function to summate the marginal rate of substitution or MRS, which is the slope of the bend at any given point. In calculus land, nosotros discover the slope of a role past calculating the first derivative. For uncomplicated one-variable functions like $x^2$, this involves moving the exponent down, multiplying information technology by the coefficient, and reducing the exponent by one. The get-go derivative of $x^ii$ is $2x$. The derivative of $2x^3$ would exist $6x^2$, and and so on.

When differentiating a two-variable function like $xy$, though, nosotros can't just follow the uncomplicated rule of moving an exponent down and subtracting one. Instead, we have to calculate fractional derivatives—we detect the derivative of simply the $x$ part while holding $y$ abiding and divide it by the derivative of merely the $y$ part while holding $x$ constant.

Don't worry if that sounds complicated. The easiest manner to do this is to go to Wolfram Alpha, type in the phrase "derivative xy" and see what it calculates for you. Y'all'll see 2 fractional derivatives: $\frac{\partial}{\partial x}$ and $\frac{\partial}{\fractional y}$. Make those two partial derivatives a ratio and yous'll have the derivative of the whole function: $\frac{\partial / \partial x}{\partial / \partial y}$. To make your life easier, I will occasionally provide you with the MRS in problem sets or exams (which I'll calculate with Wolfram Alpha because who really wants to do calculus?!).

In this instance, where $u = xy$, the slope / start derivative / MRS is $\frac{y}{10}$.

Side by side, we tin can add actual numbers to this MRS by finding the price-attuned version of the MRS. To practise this, setting the MRS equal to the ratio of the prices of waffles and calzones, since MRS tin also exist written as $\frac{\text{Price}_x}{\text{Price}_y}$):

\[ \frac{y}{x} = \frac{one}{two} \]

We can use algebra to rearrange this formula so that it's based on $y$:

\[ y = \frac{1}{ii} x \]

That is our MRS given the prices that exist in the world. Phew.

three. Set the budget line equal to the price-attuned MRS and use algebra to solve for $x$ and $y$

Now that we accept formulas for the MRT and the MRS, we tin can set up them equal to each other to find where they are tangent to each other (i.e where their slopes are the same). Algebra time!

\[ \begin{aligned} \text{Price-attuned MRS} &= \text{Budget line} \\ \frac{ane}{2} x &= -\frac{1}{ii} ten + 10 \\ ten &= 10 \end{aligned} \]

The optimal level of waffles is thus 10. We can plug that back into either the upkeep line or the MRT equation to figure out the optimal level of calzones:

\[ \begin{aligned} y &= -\frac{1}{ii} 10 + 10 \\ y &= (-\frac{ane}{2} \times ten) + ten \\ y &= v \end{aligned} \]

5 calzones! The best combination food that maximizes our utility given our budget constraint and current prices is ten waffles and 5 calzones.

Nosotros can utilise our utility part to calculate how many utils we get from that level of consumption: $u = xy$, or ten × five, or 50.

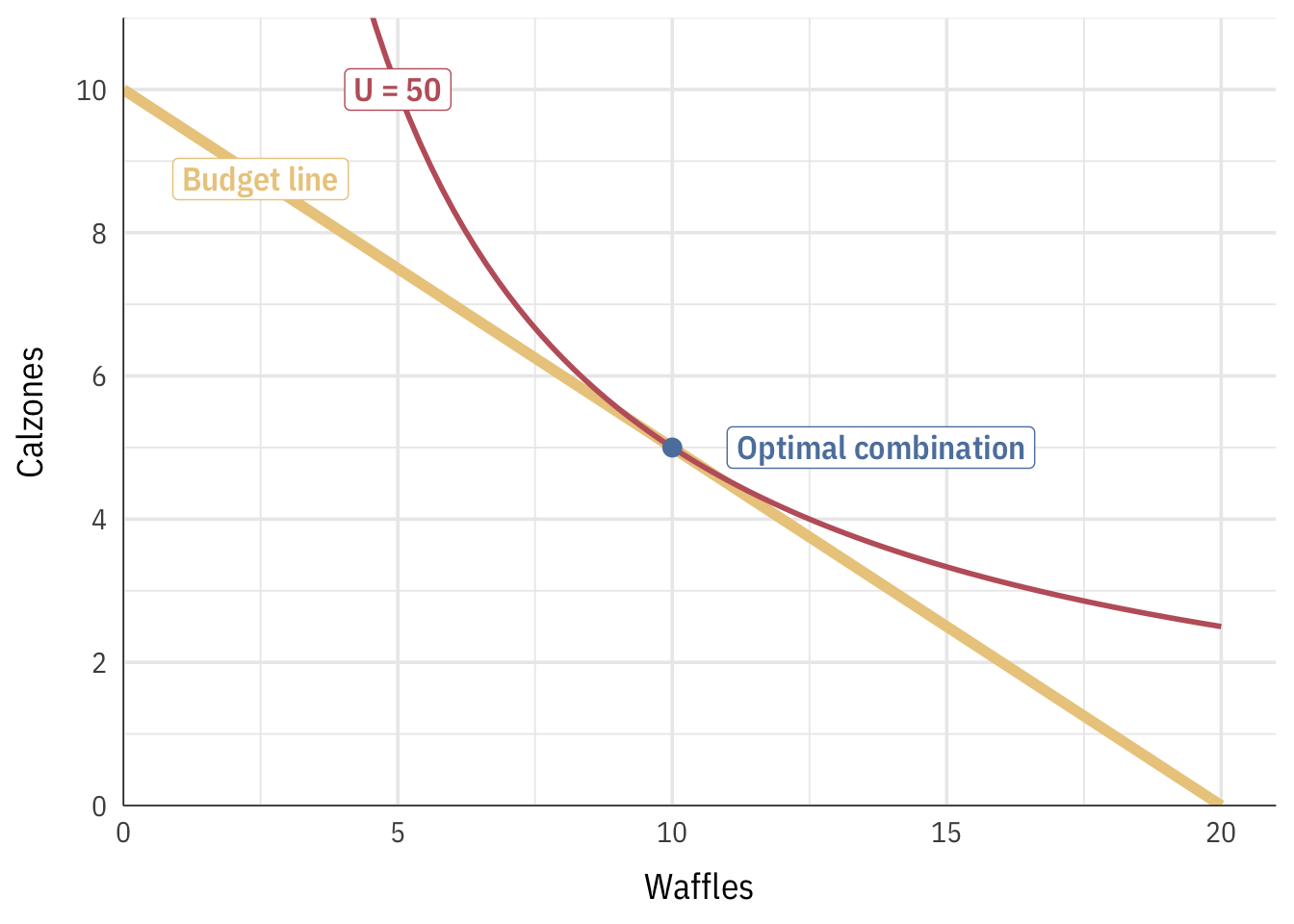
We can verify this combination graphically past plotting the budget line and indifference curve for fifty utils all at the aforementioned fourth dimension:

tl;dr Desmos version

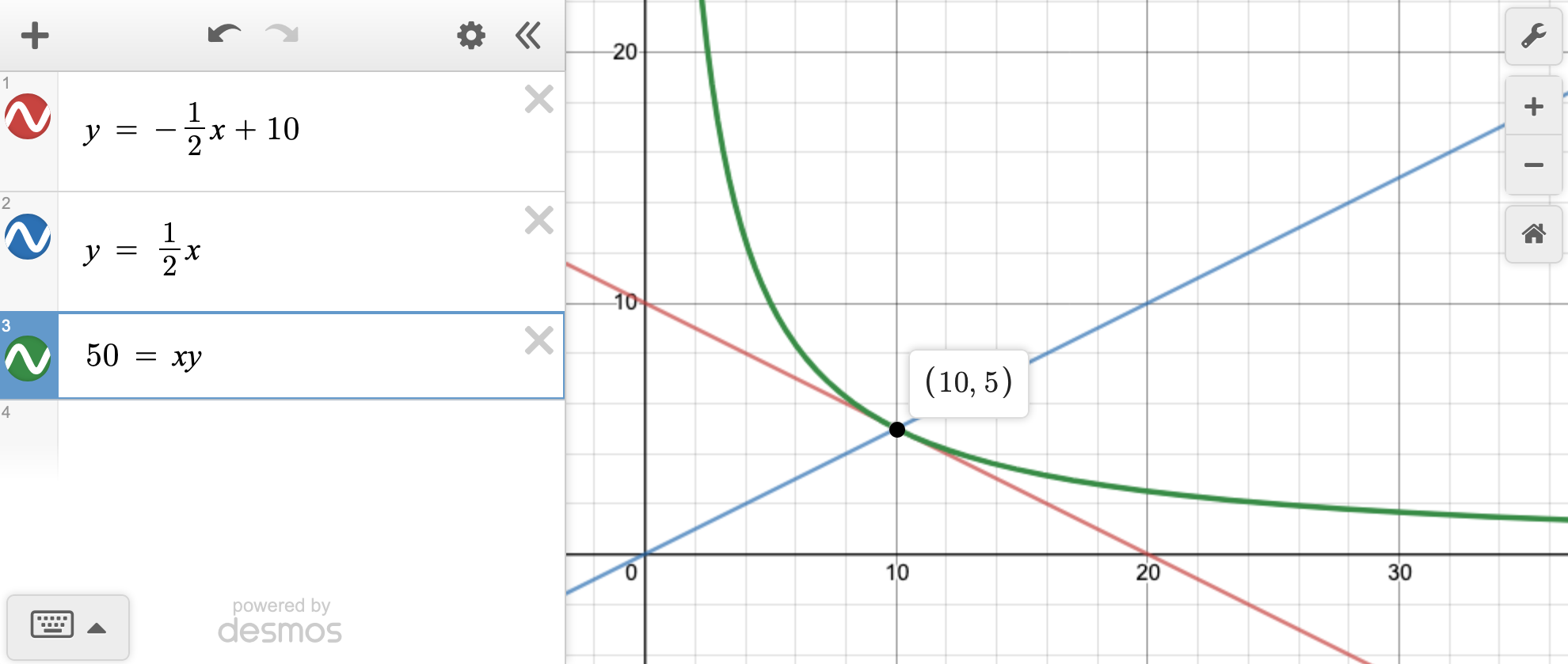
You can avoid some of the math get the same answer by plotting these formulas at Desmos or with a graphing calculator:

Figure out the budget line or feasible prepare and plot information technology: $y = -\frac{1}{2}x + 10$
Figure out the MRS ($\frac{y}{x}$), set it equal to the price ratio ($\frac{1}{2}$), and rearrange it and then that it is in terms of y: $y = \frac{1}{2} ten$. Plot that.
Notice how the 2 lines intersect at (10, 5). That's the optimal point.
Yous can add an indifference curve past figuring out what level of utility y'all get when consuming 10 waffles and five calzones (x × 5), and so plotting the utility role at that level. Yous don't need to rearrange the formula or anything; Desmos is smart plenty to figure it out: $50 = xy$.
If yous did information technology correct, you should get an indifference curve tangent to the budget line at (10, 5).

Waffles and calzones with dissimilar values

To show some additional examples of how to do this, here are a few different versions of the same question just with dissimilar prices, budgets, and utility functions.

Example 1

Here are the constraints and preferences:

Waffles ($x$) = $3
Calzones ($y$) = $six
Upkeep = $60
Utility = $u = x^ii y$

Step ane: Detect the feasible set/budget line

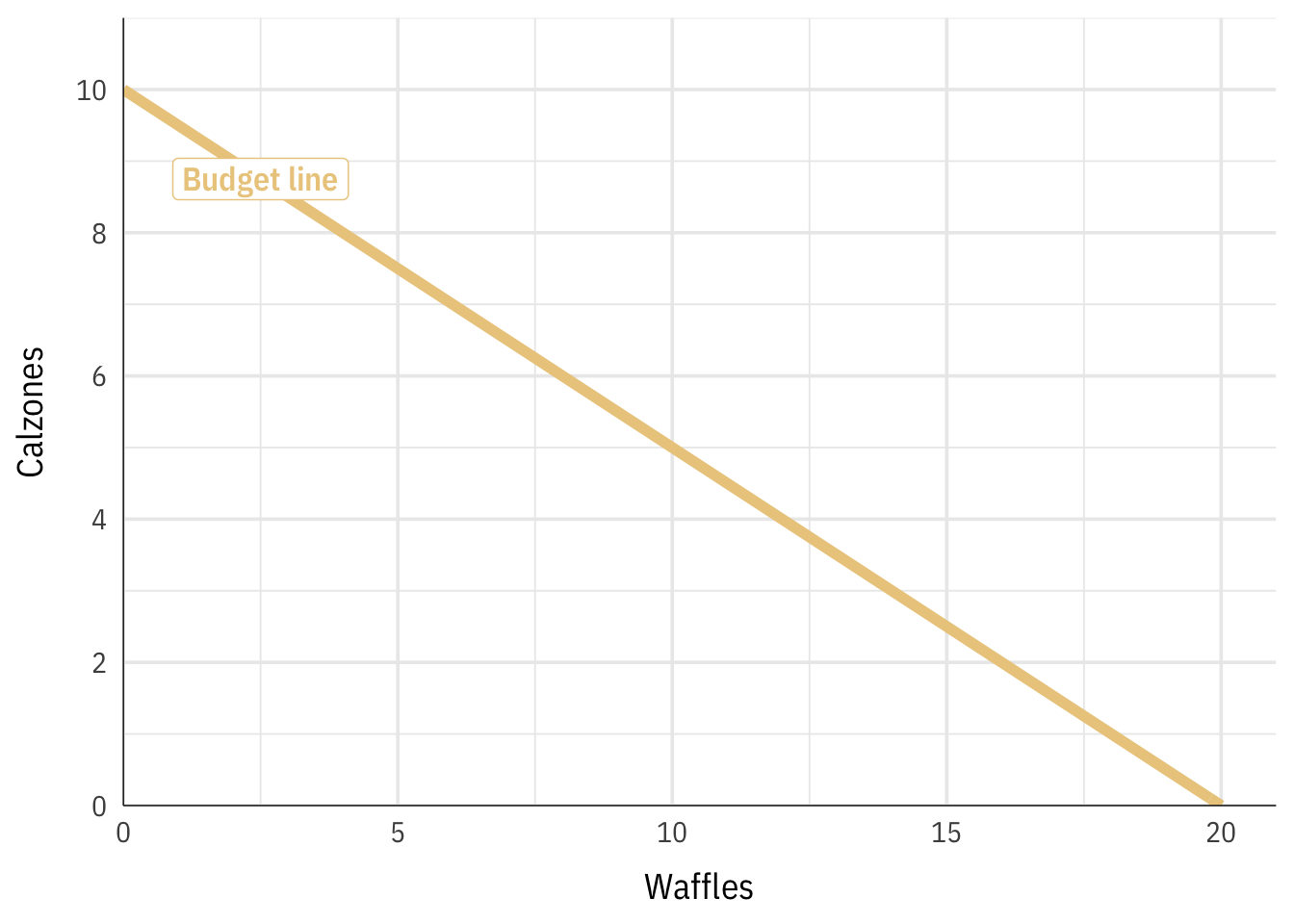
If we spent 100% of the budget on waffles, we could become xx waffles; if we spent information technology all on calzones, nosotros could get 10. That creates this upkeep line:

\[ y = -\frac{i}{2}x + 10 \]

Step 2: Find the MRS and add together prices to it

Our utility function is $u = 10^two y$. To find the gradient of this equation (or the MRS), nosotros need to notice the derivative, and because in that location are 2 variables, we need to detect the partial derivative of the $x$ part and the partial derivative of the $y$ function. Wolfram Alpha can do this for the states (blazon "derivative x^2 y"):

$\frac{\partial}{\partial x} = 2xy$
$\frac{\partial}{\partial y} = x^ii$

If we make these a ratio ($\frac{\partial / \partial ten}{\partial / \partial y}$), nosotros cease upwards with the following formula:

\[ \brainstorm{aligned} \frac{\partial / \fractional x}{\partial / \partial y} &= \frac{2xy}{x^two} \\ &= \frac{2y}{x} \end{aligned} \]

The gradient of the indifference bend at whatsoever combination of $x$ and $y$ is thus $\frac{2y}{10}$.

Next, nosotros need to build the prices into the formula by setting the MRS equal to the ratio of prices ($\frac{\text{Price}_x}{\text{Price}_y}$) and rearranging so the formula starts with $y =$:

\[ \brainstorm{aligned} \frac{2y}{10} &= \frac{three}{half dozen} \\ 12y &= 3x \\ y &= \frac{1}{4}x \end{aligned} \]

Our price-attuned MRS is thus $y = \frac{1}{4}10$.

Step iii: Set the upkeep line equal to the MRS and solve for $x$ and $y$

Finally we can fix the two equations equal to each other to find where they cross (or but put them in Desmos):

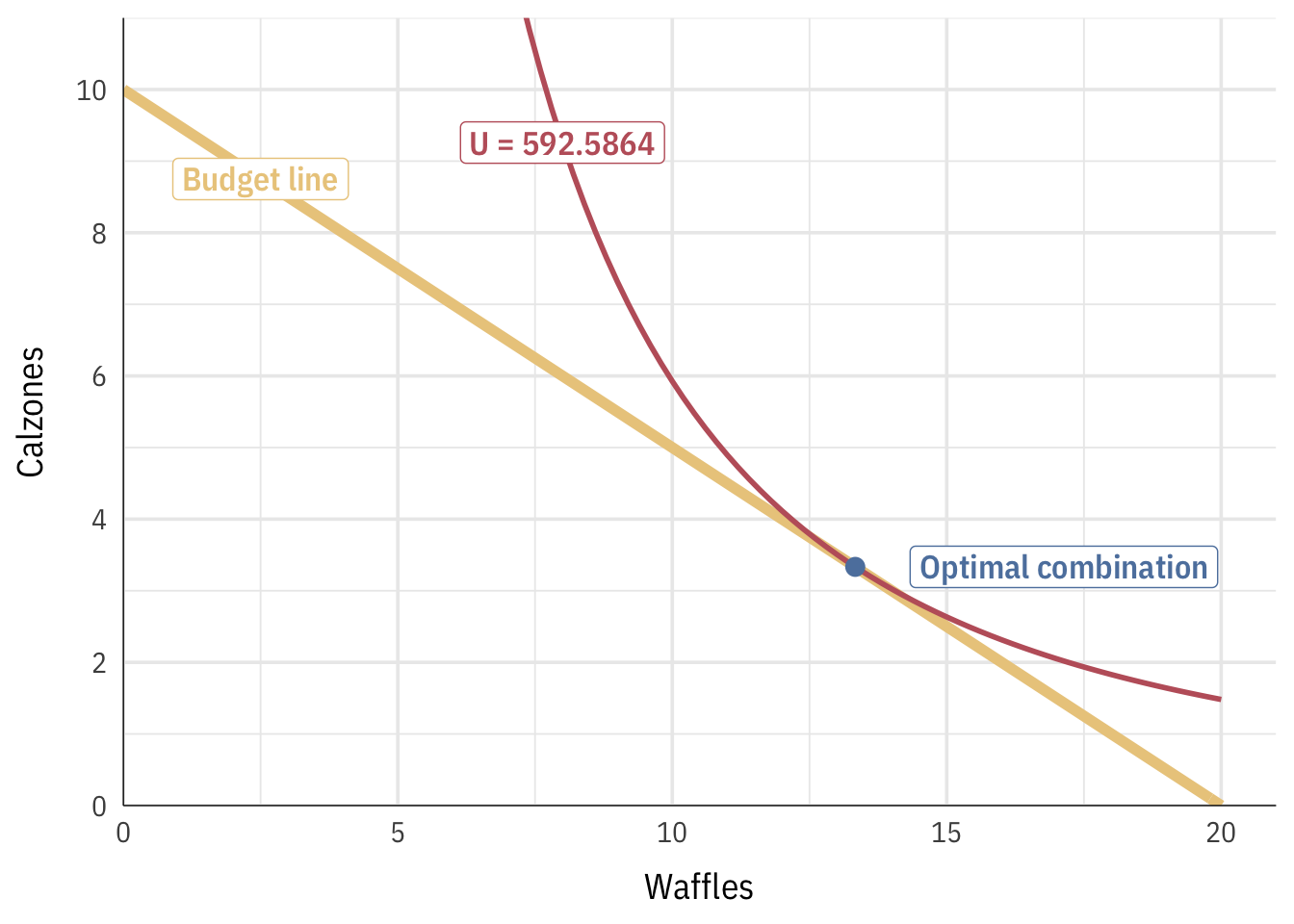
\[ \begin{aligned} -\frac{1}{2}x + 10 &= \frac{one}{iv}ten \\ x &= \frac{3x}{4} \\ xl &= 3x \\ 13.333 \text{ (or } \frac{40}{3} \text{)} &= x \cease{aligned} \] The ideal number of waffles is xiii.33. Let's plug that back into the budget line to see how many calzones nosotros can get if we get that many waffles:

\[ \begin{aligned} y &= -\frac{1}{ii} x + 10 \\ y &= -\frac{ane}{2} \times 13.333 + 10 \\ y &= 3.333 \text{ (or } \frac{10}{3} \text{)} \cease{aligned} \]

We can go 3.33 calzones. The all-time combination of waffles and calzones is thus xiii.33 and iii.33. We tin summate the utility nosotros'd become from that past plugging these values into the utility function:

\[ \brainstorm{aligned} u &= x^2 y \\ u &= 13.333^two \times 3.333 \text{ (or } \frac{40}{iii}^ii \times \frac{10}{three} \text{)} \\ u &= 592.5864 \end{aligned} \]

We'd get 592.5864 utils from xiii.333 waffles and 3.333 calzones. Hither'due south everything all together:

Example 2

Waffles ($ten$) = $3
Calzones ($y$) = $one.50
Budget = $45
Utility = $u = ten^2 \times \frac{1}{four}y$

Step 1: Find the feasible set/budget line

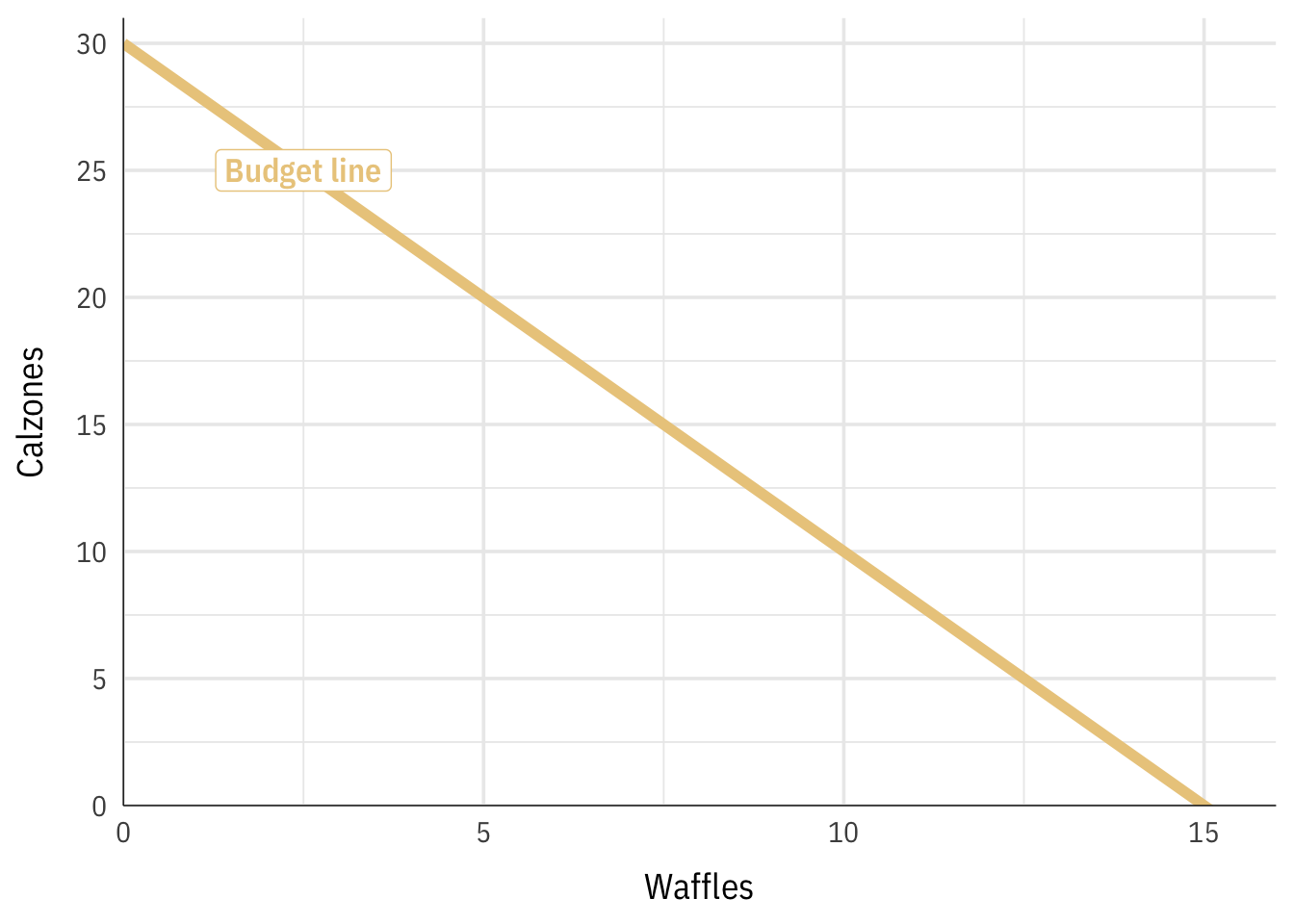
If we spent 100% of the budget on waffles, we could get 15 waffles; if nosotros spent it all on calzones, we could become xxx. That creates this budget line:

\[ y = -2x + 30 \]

Footstep 2: Find the MRS and add prices to it

Our utility office is $u = ten^2 \times \frac{1}{4}y$. To find the slope of this equation (or the MRS), we need to find the derivative, and because there are two variables, we demand to observe the partial derivative of the $x$ part and the partial derivative of the $y$ part. Wolfram Alpha can do this for us (blazon "derivative x^2 * i/4y"):

$\frac{\fractional}{\fractional x} = \frac{xy}{2}$
$\frac{\partial}{\fractional y} = \frac{ten^2}{four}$

If we make these a ratio ($\frac{\partial / \fractional x}{\partial / \partial y}$), nosotros end up with the following formula:

\[ \begin{aligned} \frac{\fractional / \fractional x}{\partial / \partial y} &= \frac{xy / 2}{x^2 / 4} \\ &= \frac{2y}{x} \end{aligned} \]

The slope of the indifference curve at any combination of $x$ and $y$ is thus $\frac{2y}{x}$.

Next, we demand to build the prices into the formula by setting the MRS equal to the ratio of prices ($\frac{\text{Price}_x}{\text{Price}_y}$) and rearranging so the formula starts with $y =$:

\[ \brainstorm{aligned} \frac{2y}{x} &= \frac{3}{1.5} \\ 3y &= 3x \\ y &= x \end{aligned} \]

Our price-attuned MRS is thus $y = x$ (that's dainty and piece of cake!).

Step 3: Prepare the upkeep line equal to the MRS and solve for $x$ and $y$

Finally we can fix the ii equations equal to each other to find where they cross (or just put them in Desmos):

\[ \begin{aligned} -2x + 30 &= x \\ xxx &= 3x \\ 10 &= x \end{aligned} \]

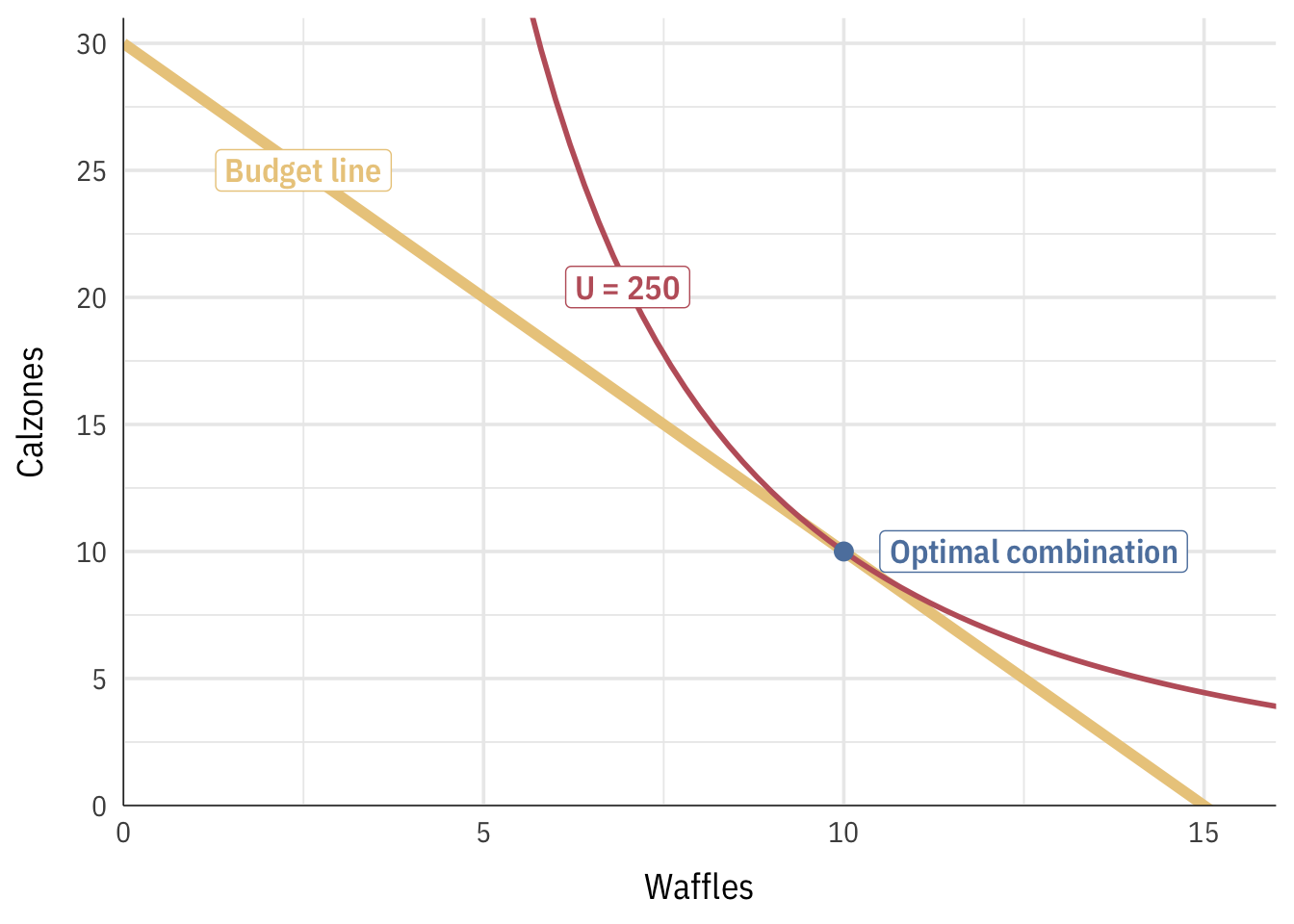
The ideal number of waffles is ten. Let's plug that dorsum into the budget line to encounter how many calzones we can get if we go that many waffles:

\[ \brainstorm{aligned} y &= -2x + 30 \\ y &= 2 \times 10 + thirty \\ y &= x \end{aligned} \]

Nosotros can get 10 calzones. The best combination of waffles and calzones is thus 10 and x. Nosotros can calculate the utility we'd get from that by plugging these values into the utility function:

\[ \begin{aligned} u &= ten^2 \times \frac{ane}{4}y \\ u &= ten^two \times (0.25 \times 10) \\ u &= 250 \stop{aligned} \]

We'd get 250 utils from ten waffles and 10 calzones. Here's everything all together:

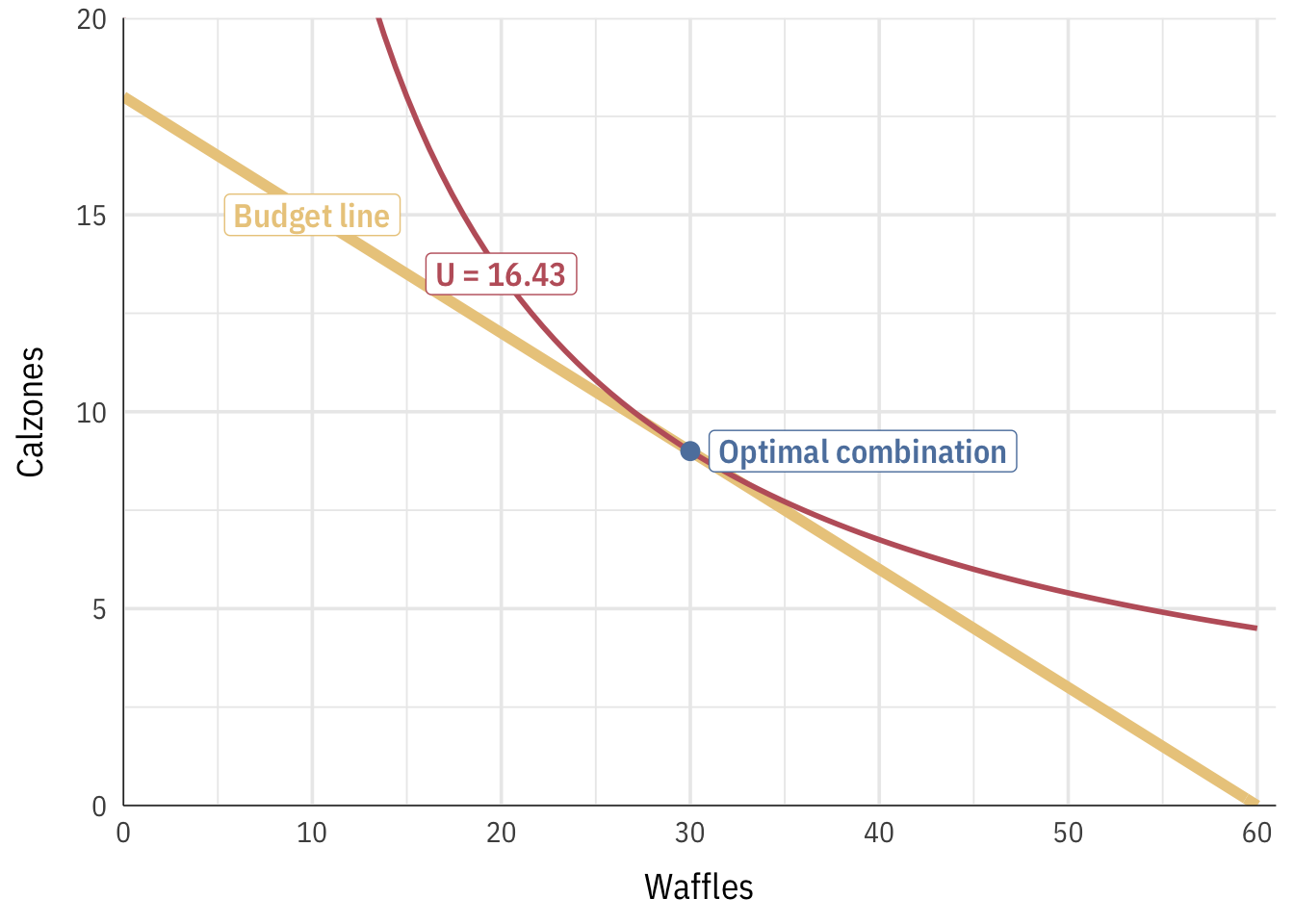
Example 3

Let's do ane more:

Waffles ($ten$) = $one.50
Calzones ($y$) = $v
Budget = $90
Utility = $u = \sqrt{xy}$

Step 1: Discover the feasible set/budget line

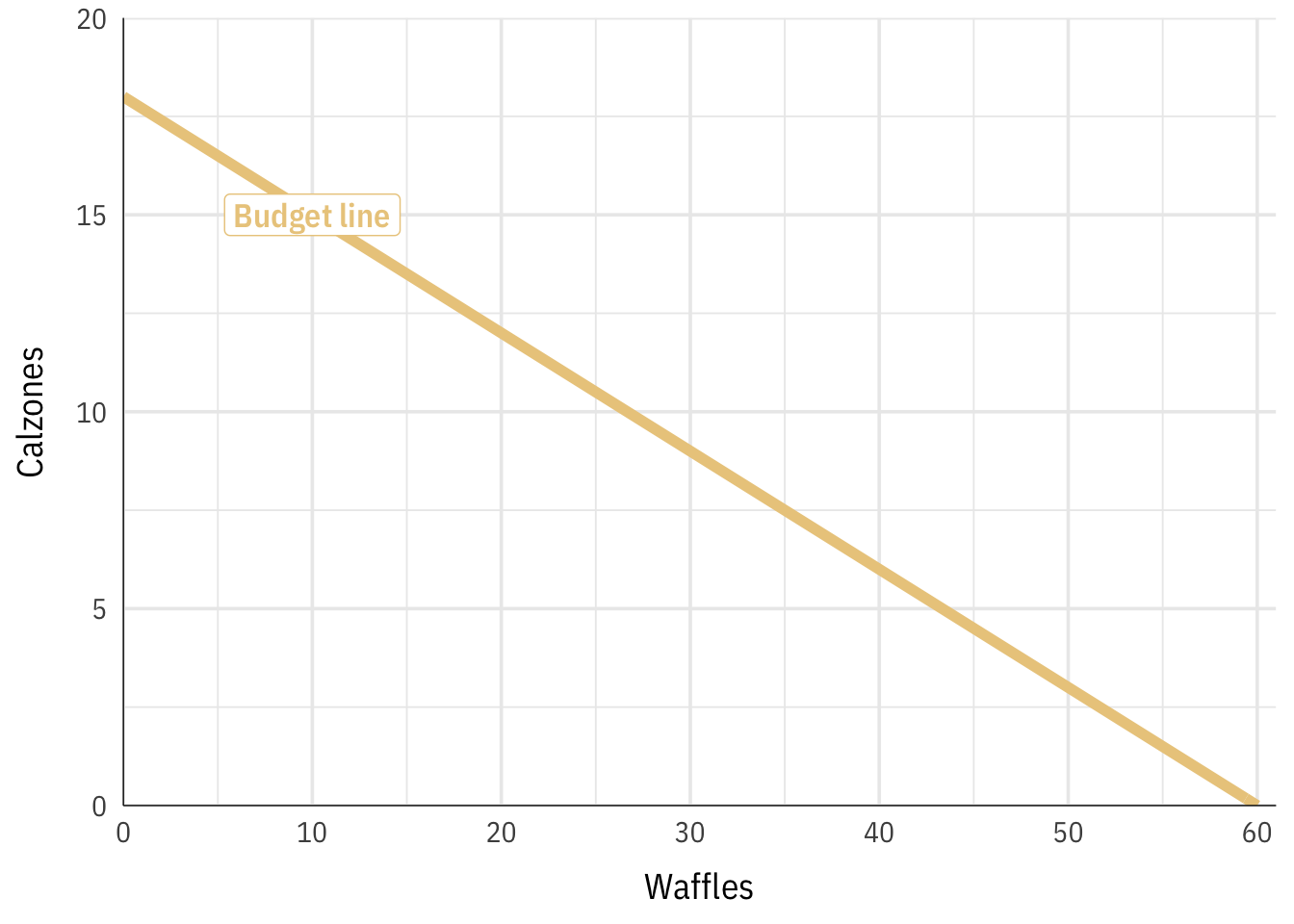
If we spent 100% of the budget on waffles, we could get sixty waffles; if we spent it all on calzones, we could get 18. That creates this budget line:

\[ y = -\frac{3}{10}x + 18 \]

Stride ii: Notice the MRS and add together prices to it

Our utility part is $u = \sqrt{ten}{y}$. To detect the slope of this equation (or the MRS), we need to find the derivative, and because there are two variables, we need to find the partial derivative of the $ten$ function and the fractional derivative of the $y$ part. Wolfram Alpha can do this for united states of america (blazon "derivative sqrt(xy)"):

$\frac{\partial}{\partial x} = \frac{y}{2 \sqrt{xy}}$
$\frac{\partial}{\fractional y} = \frac{x}{ii \sqrt{xy}}$

If nosotros make these a ratio ($\frac{\partial / \partial ten}{\partial / \partial y}$), we end upwards with the following formula:

\[ \brainstorm{aligned} \frac{\partial / \fractional x}{\partial / \partial y} &= \frac{y / 2 \sqrt{xy}}{x / 2 \sqrt{xy}} \\ &= \frac{y}{x} \end{aligned} \]

The slope of the indifference curve at whatsoever combination of $x$ and $y$ is thus $\frac{y}{10}$.

Side by side, we need to build the prices into the formula by setting the MRS equal to the ratio of prices ($\frac{\text{Price}_x}{\text{Price}_y}$) and rearranging so the formula starts with $y =$:

\[ \begin{aligned} \frac{y}{x} &= \frac{1.five}{five} \\ 5y &= 1.5x \\ y &= 0.3x \text{ (or } \frac{three}{10}x \text{)} \end{aligned} \]

Our price-attuned MRS is thus $y = 0.3x$.

Step three: Set the budget line equal to the MRS and solve for $x$ and $y$

Finally we tin ready the two equations equal to each other to find where they cross (or but put them in Desmos):

\[ \brainstorm{aligned} -\frac{3}{10}x + 18 &= \frac{3}{10}10 \\ eighteen &= \frac{6}{10}x \\ 30 &= x \terminate{aligned} \]

The ideal number of waffles is 30. Permit's plug that back into the budget line to see how many calzones we can become if we get that many waffles:

\[ \begin{aligned} y &= -\frac{iii}{x}10 + 18 \\ y &= -\frac{three}{10} \times xxx + xviii \\ y &= 9 \end{aligned} \]

We can become nine calzones. The best combination of waffles and calzones is thus 30 and nine. Nosotros tin calculate the utility we'd get from that by plugging these values into the utility function:

\[ \begin{aligned} u &= \sqrt{xy} \\ u &= \sqrt{30 \times nine} \\ u &= 16.43 \cease{aligned} \]

Nosotros'd get 16.43 utils from 30 waffles and 9 calzones. Here's everything all together: